|
|
BIOL
4120
Principles of Ecology
Phil Ganter
320
Harned Hall
963-5782
|
An immature bug on a eucalyptus leaf. |
Lecture 11 Intraspecific Population Regulation
Email me
Back to:
Overview - Link
to Course
Objectives
Logistic
Growth
In the equation for exponential
growth, the rate of population increase simply increases with N
- Not very realistic, as all populations
with an r greater than 0 would increase to infinity given infinite time
- Logistic growth is one way to
limit the population size
Logistic growth is based on the
idea of a Carrying Capacity (K)
for any environment, a population size:
- Above which the population
decreases
- Below which the population
increases
- When the population size is
at the carrying capacity, then no growth occurs
- If K is the carrying capacity
in the environment (expressed in numbers of individuals of a species) then
- produces a sigmoid curve
- hits an equilibrium value
- stable equilibrium because
the population returns to it from any other population size, given time
- logistic growth model:
- is a continuous model (notice
that what is predicted above is the growth rate, not the size of the population
- there is an equation, based on the
logistic above, for predicting population size, but we will not use
it here and so I will not present it except in the additional materials
available at Modeling Density-Dependent Growth
- is useful because it is conceptually
straightforward, although it does not accurately predict the growth of
many natural populations
- assumes that:
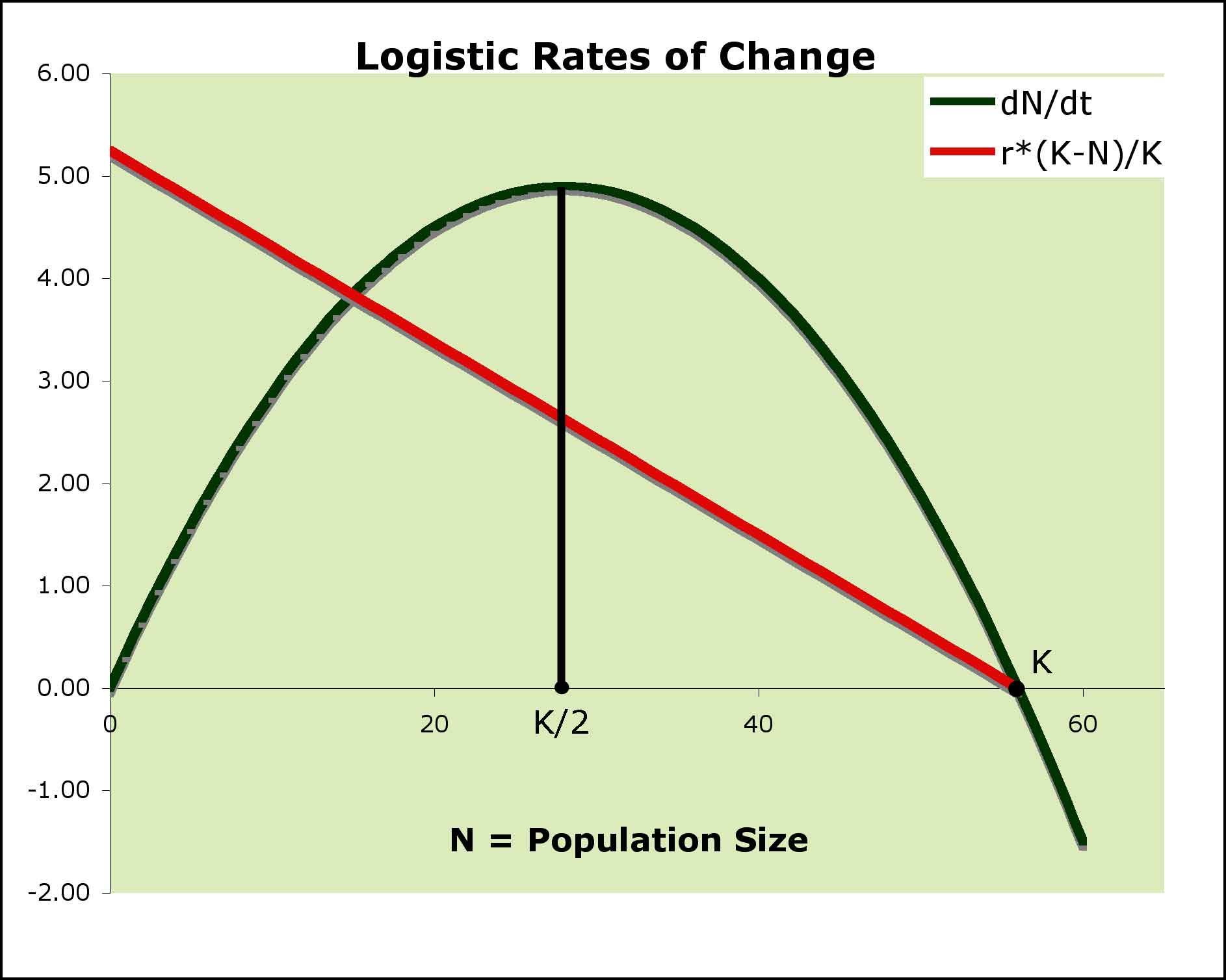
- the change in dN/dt with a change
in N is a hyperbola with a maximum (which means it is a dome and not
a valley - see graph above) at K/2
- A graph of r*(K-N)/K
versus N is a straight line which means that r is multiplied by
an ever smaller fraction, until the product of r and (K-N)/K hits
0
- The graph above shows
that the rate of population change (dN/dt) increases with N less
than K/2 but at a decreasing rate (it constantly increases in
exponential growth) until it hits a maximum at K/2 and begins
to decline after until it reaches 0 at K
- this makes sense
as the population should stop growing when it reaches its carrying
capacity, K
- for animals with complex
life histories and mating systems, the assumption of is
not always met
- social systems which
entail some individuals not breeding when they could obviously
violate this assumption
- there are no lags in the timing
of the change in dN/dt with any change in N
- lags are common when
life histories are complex, as in holometabolous insects
- larvae live in different
environment and a change in larval density may not have
an effect on egg-laying until after they pupate and become
adults
- constant K (constant environment
over space and time)
- K is likely to change
over both space and time
- constant r (all individuals equally
fit)
- often only a portion
of a population breed, the rest may be helpers or may not have
access to enough resources to breed
- no migration
- dispersal can be important,
even keeping a population from going extinct when the net replacement
rate is below 1
- Time lags introduce oscillatory
behavior into these models
- populations can cycle between
small and large values, with even intermediate levels possible
- With lags, nonlinear relationships
between dN/dt and N, and/or large r values, the models can become chaotic
For more on the logistic, including
a derivation and some problems, go to Modeling Density-Dependent Growth
Density-Dependence
vs. Density Independence and Regulation
Populations fluctuate in size and
you can always find an average population size if you have measured the population
size at two or more times.
- A question that immediately arises
about the average is whether or not the population is regulated
- Regulation
in terms of populations means that there is some population size that represents
a turning point in terms of population growth (called a set point)
- In regulated populations,
the growth rate of the population tends to be negative when the population
size is greater than the set point and positive when the population size
is smaller than the set point.
- This means that the population
grows to the set point when it is below it and declines to the set
point when it is above it.
- In Unregulated populations,
there is no relationship between population growth and population size
or, if there is a relationship, the relationship will not result in the
population size being stabilized
What mechanisms might regulate populations?
Ecologists have a general answer for this question.
- Density Dependent
influences change strength according to the density of individuals
- to regulate, the relationship
between the factor and population size must reduce population growth as
density increases
- This will be a positive
relationship for a factor that affects mortality (mortality rate increases
as population increases)
- This will be a negative
relationship for a factor that affects natality (birth rate decreases
as population increases)
- intraspecific competition
is a good example of DD effects
- Logistic is a DD model because
the population growth rate (dN/dt) is positive below K and negative above
K
- Density
Independent influences have no relation to the density of
individuals
- It is best to think of these
two things as opposite ends of a continuum, as many factors are not strongly
influenced by density, but are weakly density dependent or are density
dependent only over a particular range of densities
- DI effects often arise when
population growth rate is influenced by the abiotic
portion of an organism's environment
- Do not think that all environmental
effects are always DI
- If cold weather kills off an insect,
cold winters kill more than warm winters and, described like this,
you would expect the mortality caused by temperature to be density-independent,
since the proportion of the insects killed in the winter is not related
to population size, only temperature
- This effect may have
a DD aspect if we add some more information. If the insects
that find Refugia
(safe places) are those that survive cold weather and there are only
a limited number of places that provide refuge, when the population
size is small all find refuge and few die but, when the population
size is large not all fit into the refugia, a larger proportion of
the population will die.
- This is a DD effect because,
although cold kills, places in refugia are the limited resource that
interacts with density
Remember that density-dependent effects can be seen in both mortality rates
and in birth rates!
Intraspecific
Competition
Competition occurs when a resource
is in limited supply such that not all organisms that need it will obtain all
that they need (no limitation, no competition!)
If the organisms competing are all
members of the same population, it is Intraspecific Competition
Competition occurs in two general
ways:
Scramble
(Resource) competition
- No need for individuals
to interact directly, as each takes from a common resource
- Each competitor affects
all other competitors by reducing the amount of resource available
to others
- Schoener divided this
into:
- Exploitative -- consumption of the
same food item or abiotic resource
- Preemptive -- taking space on a surface
needed for living (rocks for mussels, land for plants, etc.)
Interference
(Contest) competition
- Competitors interact
directly, outcome of one contest need not affect any other competitors
- Competition for territory
- Inhibitory chemicals
- Contests for individual
resource items (crocs and lions!)
More
Mechanisms of Density-Dependent Regulation
Density dependent effects can be
seen in many aspects of life history
Density-Dependent
Dispersal
- Rather than die or fail to reproduce,
organisms often leave
- Density-dependent dispersal has
the potential to be an important regulatory mechanism
- Has not often been detected in
natural situations
Social
Behavior
- Some animals live in Social Groups,
where individuals interact and cooperate in obtaining food and in reproduction
- Social groups are often Kin Groups
of related individuals
- Group size often responds to
the availability of resources, such that there are many small reproducing
groups when resources are plentiful and fewer reproducing groups when resources
are scarce
Territoriality
- Animals have Home Ranges, areas
they use in a year's activity
- In some cases, ranges are defended
from incursion of other competitors and they become Territories
- Territories represent a division
of resources and may determine reproductive success
Plant
Mechanisms
- Just a note on competition from
the viewpoint of a plant
- Plants compete with immediate
neighbors for
- Sunlight (shading is a competitive
mechanism)
- Soil Minerals (plants may
secrete chemicals that inhibit the growth of other plant's roots and,
in that manner, secure access to resources)
- Sessile animals (sponges, corals,
etc.) may compete in ways similar to the ways in which plants compete
Terms
Logistic Growth,
Carrying Capacity (K), Regulation, Density
Dependent, Density Independent,
Abiotic, Refugia, Intraspecific Competition, Scramble (Resource) competition,
Interference (Contest) competition, Density-Dependent Dispersal, Social Behavior,
Territoriality
Last updated March 2, 2007